Note
Go to the end to download the full example code
Example: Gaussian Process¶
In this example we show how to use NUTS to sample from the posterior over the hyperparameters of a gaussian process.
import argparse
import os
import time
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import jax
from jax import vmap
import jax.numpy as jnp
import jax.random as random
import numpyro
import numpyro.distributions as dist
from numpyro.infer import (
MCMC,
NUTS,
init_to_feasible,
init_to_median,
init_to_sample,
init_to_uniform,
init_to_value,
)
matplotlib.use("Agg") # noqa: E402
# squared exponential kernel with diagonal noise term
def kernel(X, Z, var, length, noise, jitter=1.0e-6, include_noise=True):
deltaXsq = jnp.power((X[:, None] - Z) / length, 2.0)
k = var * jnp.exp(-0.5 * deltaXsq)
if include_noise:
k += (noise + jitter) * jnp.eye(X.shape[0])
return k
def model(X, Y):
# set uninformative log-normal priors on our three kernel hyperparameters
var = numpyro.sample("kernel_var", dist.LogNormal(0.0, 10.0))
noise = numpyro.sample("kernel_noise", dist.LogNormal(0.0, 10.0))
length = numpyro.sample("kernel_length", dist.LogNormal(0.0, 10.0))
# compute kernel
k = kernel(X, X, var, length, noise)
# sample Y according to the standard gaussian process formula
numpyro.sample(
"Y",
dist.MultivariateNormal(loc=jnp.zeros(X.shape[0]), covariance_matrix=k),
obs=Y,
)
# helper function for doing hmc inference
def run_inference(model, args, rng_key, X, Y):
start = time.time()
# demonstrate how to use different HMC initialization strategies
if args.init_strategy == "value":
init_strategy = init_to_value(
values={"kernel_var": 1.0, "kernel_noise": 0.05, "kernel_length": 0.5}
)
elif args.init_strategy == "median":
init_strategy = init_to_median(num_samples=10)
elif args.init_strategy == "feasible":
init_strategy = init_to_feasible()
elif args.init_strategy == "sample":
init_strategy = init_to_sample()
elif args.init_strategy == "uniform":
init_strategy = init_to_uniform(radius=1)
kernel = NUTS(model, init_strategy=init_strategy)
mcmc = MCMC(
kernel,
num_warmup=args.num_warmup,
num_samples=args.num_samples,
num_chains=args.num_chains,
thinning=args.thinning,
progress_bar=False if "NUMPYRO_SPHINXBUILD" in os.environ else True,
)
mcmc.run(rng_key, X, Y)
mcmc.print_summary()
print("\nMCMC elapsed time:", time.time() - start)
return mcmc.get_samples()
# do GP prediction for a given set of hyperparameters. this makes use of the well-known
# formula for Gaussian process predictions
def predict(rng_key, X, Y, X_test, var, length, noise, use_cholesky=True):
# compute kernels between train and test data, etc.
k_pp = kernel(X_test, X_test, var, length, noise, include_noise=True)
k_pX = kernel(X_test, X, var, length, noise, include_noise=False)
k_XX = kernel(X, X, var, length, noise, include_noise=True)
# since K_xx is symmetric positive-definite, we can use the more efficient and
# stable Cholesky decomposition instead of matrix inversion
if use_cholesky:
K_xx_cho = jax.scipy.linalg.cho_factor(k_XX)
K = k_pp - jnp.matmul(k_pX, jax.scipy.linalg.cho_solve(K_xx_cho, k_pX.T))
mean = jnp.matmul(k_pX, jax.scipy.linalg.cho_solve(K_xx_cho, Y))
else:
K_xx_inv = jnp.linalg.inv(k_XX)
K = k_pp - jnp.matmul(k_pX, jnp.matmul(K_xx_inv, jnp.transpose(k_pX)))
mean = jnp.matmul(k_pX, jnp.matmul(K_xx_inv, Y))
sigma_noise = jnp.sqrt(jnp.clip(jnp.diag(K), a_min=0.0)) * jax.random.normal(
rng_key, X_test.shape[:1]
)
# we return both the mean function and a sample from the posterior predictive for the
# given set of hyperparameters
return mean, mean + sigma_noise
# create artificial regression dataset
def get_data(N=30, sigma_obs=0.15, N_test=400):
np.random.seed(0)
X = jnp.linspace(-1, 1, N)
Y = X + 0.2 * jnp.power(X, 3.0) + 0.5 * jnp.power(0.5 + X, 2.0) * jnp.sin(4.0 * X)
Y += sigma_obs * np.random.randn(N)
Y -= jnp.mean(Y)
Y /= jnp.std(Y)
assert X.shape == (N,)
assert Y.shape == (N,)
X_test = jnp.linspace(-1.3, 1.3, N_test)
return X, Y, X_test
def main(args):
X, Y, X_test = get_data(N=args.num_data)
# do inference
rng_key, rng_key_predict = random.split(random.PRNGKey(0))
samples = run_inference(model, args, rng_key, X, Y)
# do prediction
vmap_args = (
random.split(rng_key_predict, samples["kernel_var"].shape[0]),
samples["kernel_var"],
samples["kernel_length"],
samples["kernel_noise"],
)
means, predictions = vmap(
lambda rng_key, var, length, noise: predict(
rng_key, X, Y, X_test, var, length, noise, use_cholesky=args.use_cholesky
)
)(*vmap_args)
mean_prediction = np.mean(means, axis=0)
percentiles = np.percentile(predictions, [5.0, 95.0], axis=0)
# make plots
fig, ax = plt.subplots(figsize=(8, 6), constrained_layout=True)
# plot training data
ax.plot(X, Y, "kx")
# plot 90% confidence level of predictions
ax.fill_between(X_test, percentiles[0, :], percentiles[1, :], color="lightblue")
# plot mean prediction
ax.plot(X_test, mean_prediction, "blue", ls="solid", lw=2.0)
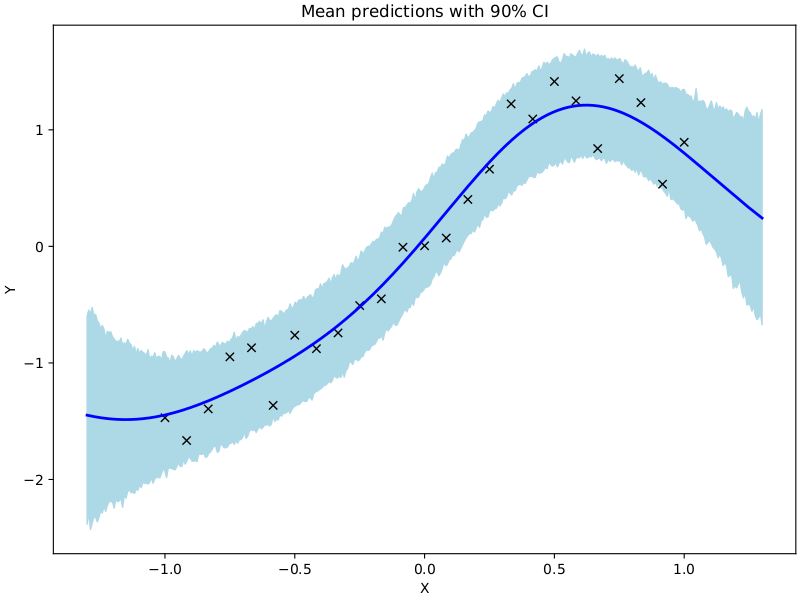
ax.set(xlabel="X", ylabel="Y", title="Mean predictions with 90% CI")
plt.savefig("gp_plot.pdf")
if __name__ == "__main__":
assert numpyro.__version__.startswith("0.14.0")
parser = argparse.ArgumentParser(description="Gaussian Process example")
parser.add_argument("-n", "--num-samples", nargs="?", default=1000, type=int)
parser.add_argument("--num-warmup", nargs="?", default=1000, type=int)
parser.add_argument("--num-chains", nargs="?", default=1, type=int)
parser.add_argument("--thinning", nargs="?", default=2, type=int)
parser.add_argument("--num-data", nargs="?", default=25, type=int)
parser.add_argument("--device", default="cpu", type=str, help='use "cpu" or "gpu".')
parser.add_argument(
"--init-strategy",
default="median",
type=str,
choices=["median", "feasible", "value", "uniform", "sample"],
)
parser.add_argument("--no-cholesky", dest="use_cholesky", action="store_false")
args = parser.parse_args()
numpyro.set_platform(args.device)
numpyro.set_host_device_count(args.num_chains)
main(args)