Bayesian Censoring Data Modeling¶
In this example we show how to model censored data using NumPyro. Censoring is a condition in which the value of a measurement or observation is only partially known. We work out two examples: a continuous and a discrete likelihood. Both cases follow the same structure but differ in a small detail, which we want to highlight. The key ingredient of the modeling strategy is the cumulative distribution function (CDF) parametrization described in Uber’s blog post “Modeling Censored Time-to-Event Data Using Pyro, an Open Source Probabilistic Programming Language” (see here the original gist code).
This example is based in the notebook Bayesian Censoring Data Modeling.
Prepare Notebook¶
[ ]:
!pip install -q numpyro@git+https://github.com/pyro-ppl/numpyro arviz matplotlib preliz pydantic
[ ]:
import os
import arviz as az
from IPython.display import set_matplotlib_formats
from jaxlib.xla_extension import ArrayImpl
import matplotlib.pyplot as plt
import preliz as pz
from pydantic import BaseModel, Field
from jax import random
import jax.numpy as jnp
import numpyro
import numpyro.distributions as dist
from numpyro.handlers import mask
from numpyro.infer import MCMC, NUTS, Predictive
plt.style.use("bmh")
if "NUMPYRO_SPHINXBUILD" in os.environ:
set_matplotlib_formats("svg")
plt.rcParams["figure.figsize"] = [8, 6]
numpyro.set_host_device_count(n=4)
rng_key = random.PRNGKey(seed=0)
assert numpyro.__version__.startswith("0.14.0")
%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = "retina"
Part I: Continuous Distribution¶
We start by considering the continuous case. We assume that we have a dataset of observations \(y\) that are censored from below and above at a known thresholds. We want to estimate the parameters of a distribution that generated these observations. We assume that the distribution is a gamma distribution (with parameters \(\alpha\) and \(\beta\)), but the same approach can be used for other distributions.
Generate Censored Data¶
We generate data from a gamma distribution and we clip the data to be between the thresholds lower and upper. We then plot the histogram of the data and the true gamma distribution.
[2]:
class CensoredGammaDataParams(BaseModel):
alpha: float = Field(..., description="Concentration parameter", gt=0)
beta: float = Field(..., description="Rate parameter", gt=0)
lower: float = Field(..., description="Lower censoring bound", gt=0)
upper: float = Field(..., description="Upper censoring bound", gt=0)
n: int = Field(..., description="Number of samples", gt=0)
def generate_censored_gamma_samples(
rng_key: ArrayImpl, params: CensoredGammaDataParams
) -> ArrayImpl:
raw_samples = dist.Gamma(concentration=params.alpha, rate=params.beta).sample(
rng_key, (params.n,)
)
return jnp.clip(raw_samples, params.lower, params.upper)
censored_gamma_data_params = CensoredGammaDataParams(
alpha=3.0, beta=1.0, lower=0.5, upper=5.0, n=100
)
rng_key, rng_subkey = random.split(rng_key)
censored_gamma_samples = generate_censored_gamma_samples(
rng_key=rng_subkey, params=censored_gamma_data_params
)
fig, ax = plt.subplots()
_ = ax.hist(
censored_gamma_samples,
bins=20,
density=True,
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_gamma_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_gamma_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Gamma(
alpha=censored_gamma_data_params.alpha, beta=censored_gamma_data_params.beta
).plot_pdf(color="C0", ax=ax)
ax.set_title("Censored Gamma Sample Data", fontsize=16, fontweight="bold");
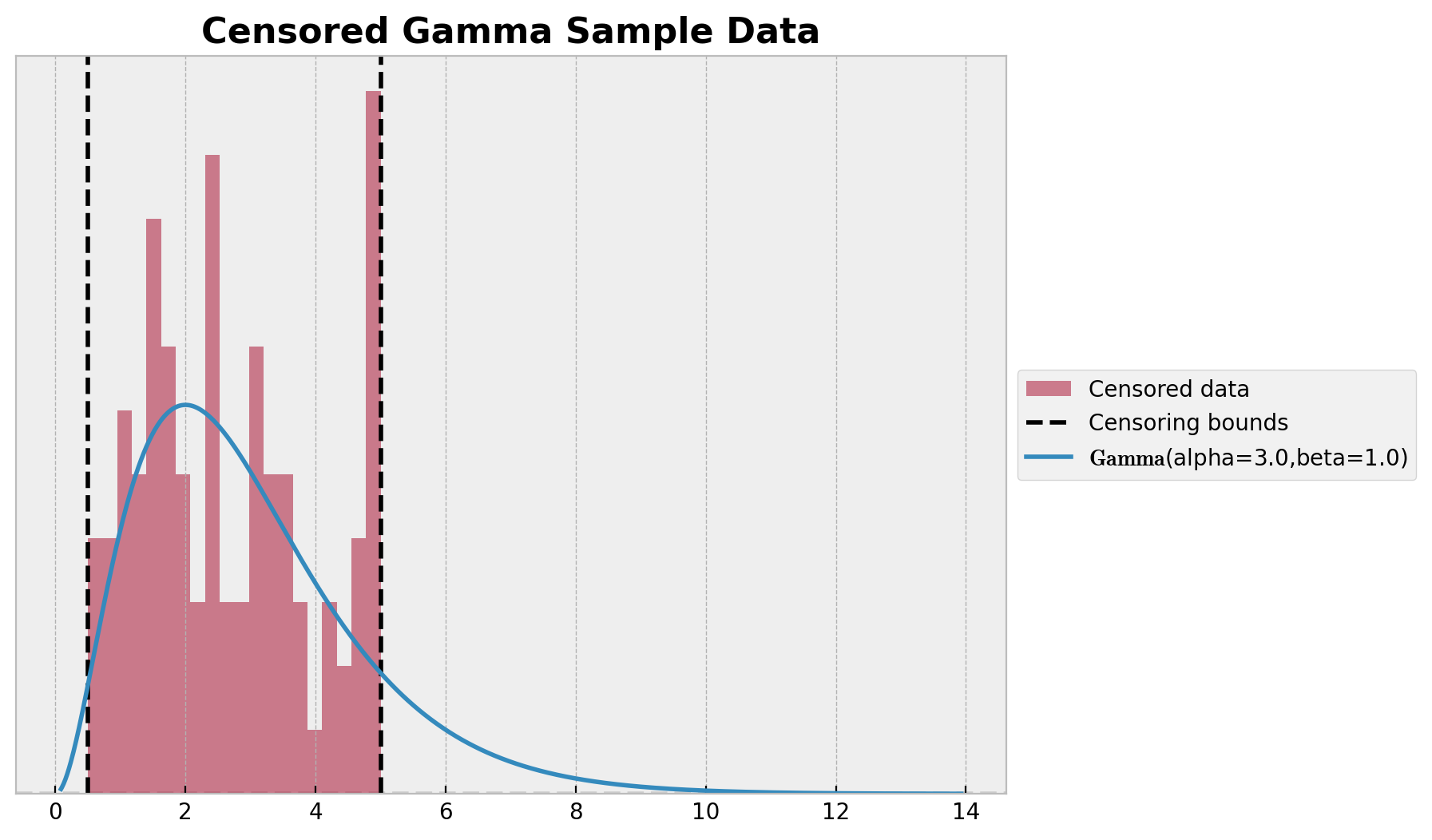
Naive Model¶
Before we implement the censoring model, we start with a naive model that does not take into account the censoring component. We simply use a gamma distribution with parameters \(\alpha\) and \(\beta\) to model the data. We then plot the posterior distribution of the parameters and compare them with the true values.
[3]:
def gamma_model(y: ArrayImpl) -> None:
alpha = numpyro.sample("alpha", dist.Exponential(1.0))
beta = numpyro.sample("beta", dist.Exponential(1.0))
numpyro.sample("obs", dist.Gamma(concentration=alpha, rate=beta), obs=y)
class InferenceParams(BaseModel):
num_warmup: int = Field(2_000, ge=1)
num_samples: int = Field(3_000, ge=1)
num_chains: int = Field(4, ge=1)
inference_params = InferenceParams()
gamma_kernel = NUTS(gamma_model)
gamma_mcmc = MCMC(
gamma_kernel,
num_warmup=inference_params.num_warmup,
num_samples=inference_params.num_samples,
num_chains=inference_params.num_chains,
)
rng_key, rng_subkey = random.split(rng_key)
gamma_mcmc.run(rng_key, y=censored_gamma_samples)
Compiling.. : 0%| | 0/5000 [00:00<?, ?it/s]
Running chain 0: 0%| | 0/5000 [00:02<?, ?it/s]
Running chain 0: 100%|██████████| 5000/5000 [00:03<00:00, 1644.63it/s]
Running chain 1: 100%|██████████| 5000/5000 [00:03<00:00, 1648.12it/s]
Running chain 2: 100%|██████████| 5000/5000 [00:03<00:00, 1657.49it/s]
Running chain 3: 100%|██████████| 5000/5000 [00:02<00:00, 1674.47it/s]
We also generate posterior predictive samples.
[4]:
gamma_predictive = Predictive(
model=gamma_model, posterior_samples=gamma_mcmc.get_samples()
)
rng_key, rng_subkey = random.split(rng_key)
gamma_posterior_predictive = gamma_predictive(rng_subkey, y=None)
gamma_idata = az.from_numpyro(posterior=gamma_mcmc)
gamma_idata.extend(az.from_numpyro(posterior_predictive=gamma_posterior_predictive))
Now we plot the trace and compare the true and estimated parameters.
[5]:
axes = az.plot_trace(
data=gamma_idata,
compact=True,
lines=[
("alpha", {}, censored_gamma_data_params.alpha),
("beta", {}, censored_gamma_data_params.beta),
],
backend_kwargs={"figsize": (10, 6), "layout": "constrained"},
)
plt.gcf().suptitle("Gamma Model", fontsize=18, fontweight="bold");
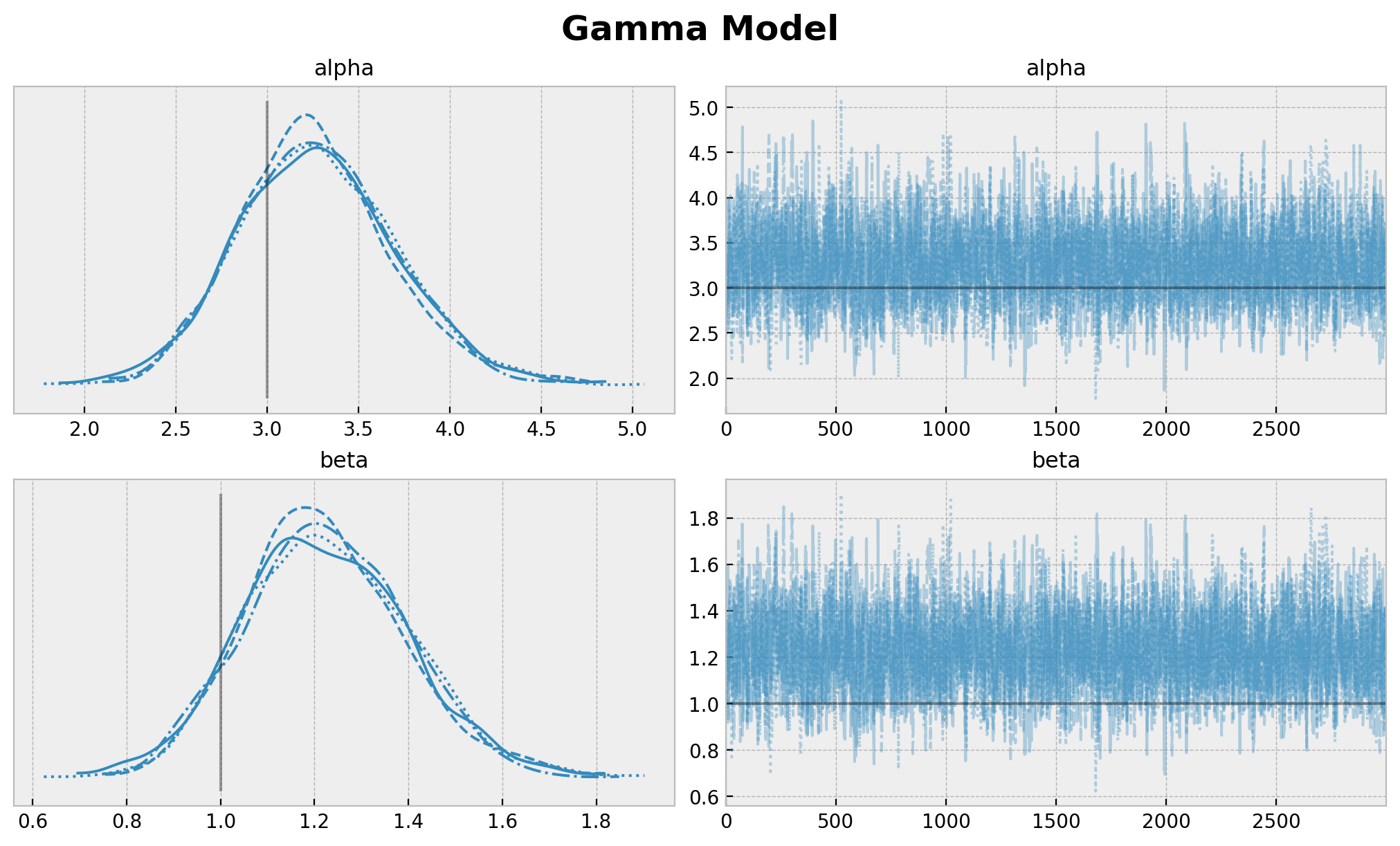
[6]:
axes = az.plot_posterior(
data=gamma_idata,
ref_val=[censored_gamma_data_params.alpha, censored_gamma_data_params.beta],
round_to=3,
figsize=(12, 5),
)
plt.gcf().suptitle("Gamma Model Parameters", fontsize=18, fontweight="bold", y=1.03);
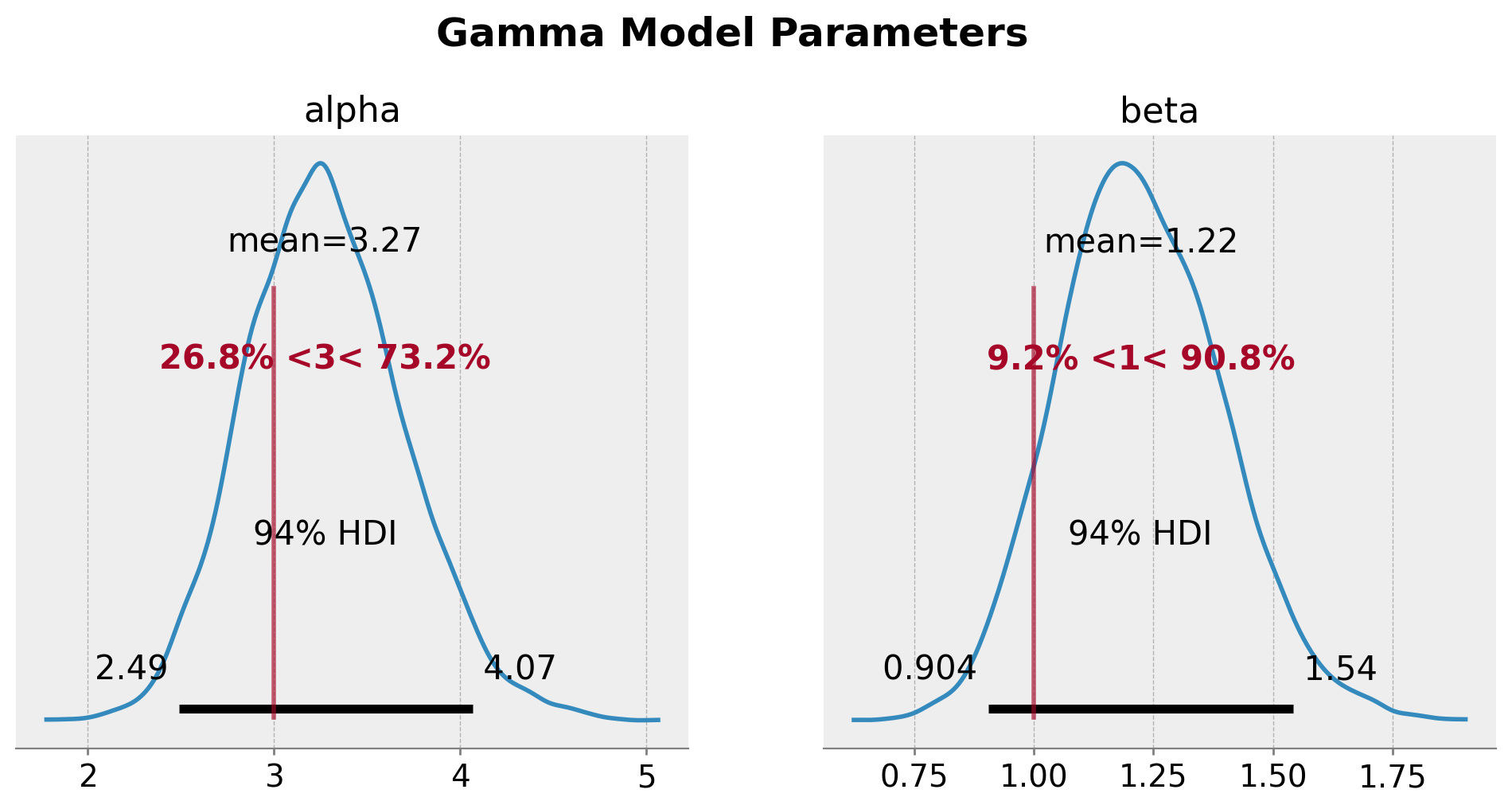
Despite the fact that the true parameters are in the \(94\%\) HDI, we do see a bias in the estimation of the parameters. This is expected since we are not taking into account the censoring in the model.
We can visualize the inferred distribution and compare it with the true distribution from the data generating process.
[7]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_gamma_samples,
bins=20,
density=True,
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_gamma_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_gamma_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Gamma(
alpha=censored_gamma_data_params.alpha, beta=censored_gamma_data_params.beta
).plot_pdf(color="C0", ax=ax)
az.plot_kde(
gamma_idata["posterior_predictive"]["obs"].to_numpy().flatten(),
plot_kwargs={"color": "C2", "label": "Posterior predictive"},
ax=ax,
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Gamma Model", fontsize=16, fontweight="bold");
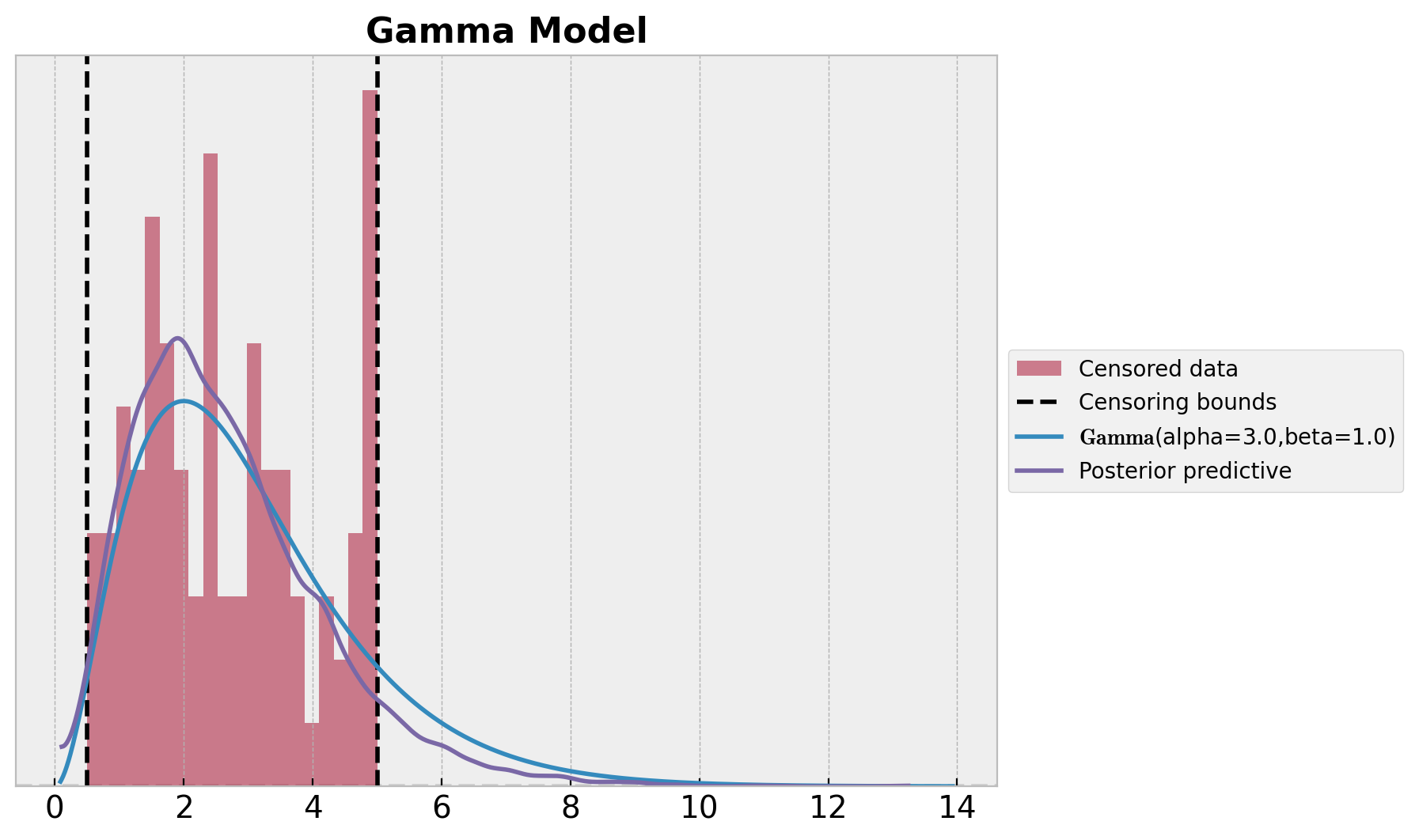
Here see that the distributions do not match well.
Censored Gamma Model¶
As mentioned in the introduction, the main idea to implement the censoring model is to use the CDF parametrization. The reason is because the probability density function PDF of a censored distribution is
Hence, we just need too implement these conditions as a custom likelihood function. To do this in NumPyro we follow the approach described in the gist of Uber’s blog post. To follow this strategy we need an indicator function to encode the censoring:
[8]:
def get_truncation_label(y: ArrayImpl, lower: float, upper: float) -> ArrayImpl:
return jnp.where(y == lower, -1, jnp.where(y == upper, 1, 0))
truncation_label = get_truncation_label(
y=censored_gamma_samples,
lower=censored_gamma_data_params.lower,
upper=censored_gamma_data_params.upper,
)
We are now ready to implement the model. For points in the interval \(lower < y < upper\) we simply sample form a gamma distribution. On the other hand, points on the boundary follow Bernoulli distribution (if we model the censoring mask value) where the truncation probability can be parametrized by the CDF. Let’s see how to do this concretely:
[9]:
def censored_gamma_model(
y: ArrayImpl, lower: float, upper: float, truncation_label: ArrayImpl
) -> None:
alpha = numpyro.sample("alpha", dist.Exponential(1.0))
beta = numpyro.sample("beta", dist.Exponential(1.0))
distribution = dist.Gamma(concentration=alpha, rate=beta)
with mask(mask=truncation_label == -1):
truncation_prob_lower = distribution.cdf(lower)
numpyro.sample(
"truncated_label_lower", dist.Bernoulli(truncation_prob_lower), obs=1
)
with mask(mask=truncation_label == 0):
numpyro.sample("obs", distribution, obs=y)
with mask(mask=truncation_label == 1):
truncation_prob_upper = 1 - distribution.cdf(upper)
numpyro.sample(
"truncated_label_upper", dist.Bernoulli(truncation_prob_upper), obs=1
)
[10]:
censored_gamma_kernel = NUTS(censored_gamma_model)
censored_gamma_mcmc = MCMC(
censored_gamma_kernel,
num_warmup=inference_params.num_warmup,
num_samples=inference_params.num_samples,
num_chains=inference_params.num_chains,
)
rng_key, rng_subkey = random.split(rng_key)
censored_gamma_mcmc.run(
rng_key,
y=censored_gamma_samples,
lower=censored_gamma_data_params.lower,
upper=censored_gamma_data_params.upper,
truncation_label=truncation_label,
)
Compiling.. : 0%| | 0/5000 [00:00<?, ?it/s]
Running chain 0: 100%|██████████| 5000/5000 [00:04<00:00, 1028.68it/s]
Running chain 1: 100%|██████████| 5000/5000 [00:04<00:00, 1029.09it/s]
Running chain 2: 100%|██████████| 5000/5000 [00:04<00:00, 1029.55it/s]
Running chain 3: 100%|██████████| 5000/5000 [00:04<00:00, 1030.11it/s]
Remark: Note that is straightforward to add lower and upper censoring components to the model (Uber’s blog post has just one censoring component).
We now fit the model and evaluate the results:
[11]:
censored_gamma_predictive = Predictive(
model=censored_gamma_model,
posterior_samples=censored_gamma_mcmc.get_samples(),
return_sites=["obs"],
)
rng_key, rng_subkey = random.split(rng_key)
censored_gamma_posterior_predictive = censored_gamma_predictive(
rng_subkey,
y=None,
lower=censored_gamma_data_params.lower,
upper=censored_gamma_data_params.upper,
truncation_label=truncation_label,
)
censored_gamma_idata = az.from_numpyro(posterior=censored_gamma_mcmc)
censored_gamma_idata.extend(
az.from_numpyro(posterior_predictive=censored_gamma_posterior_predictive)
)
[12]:
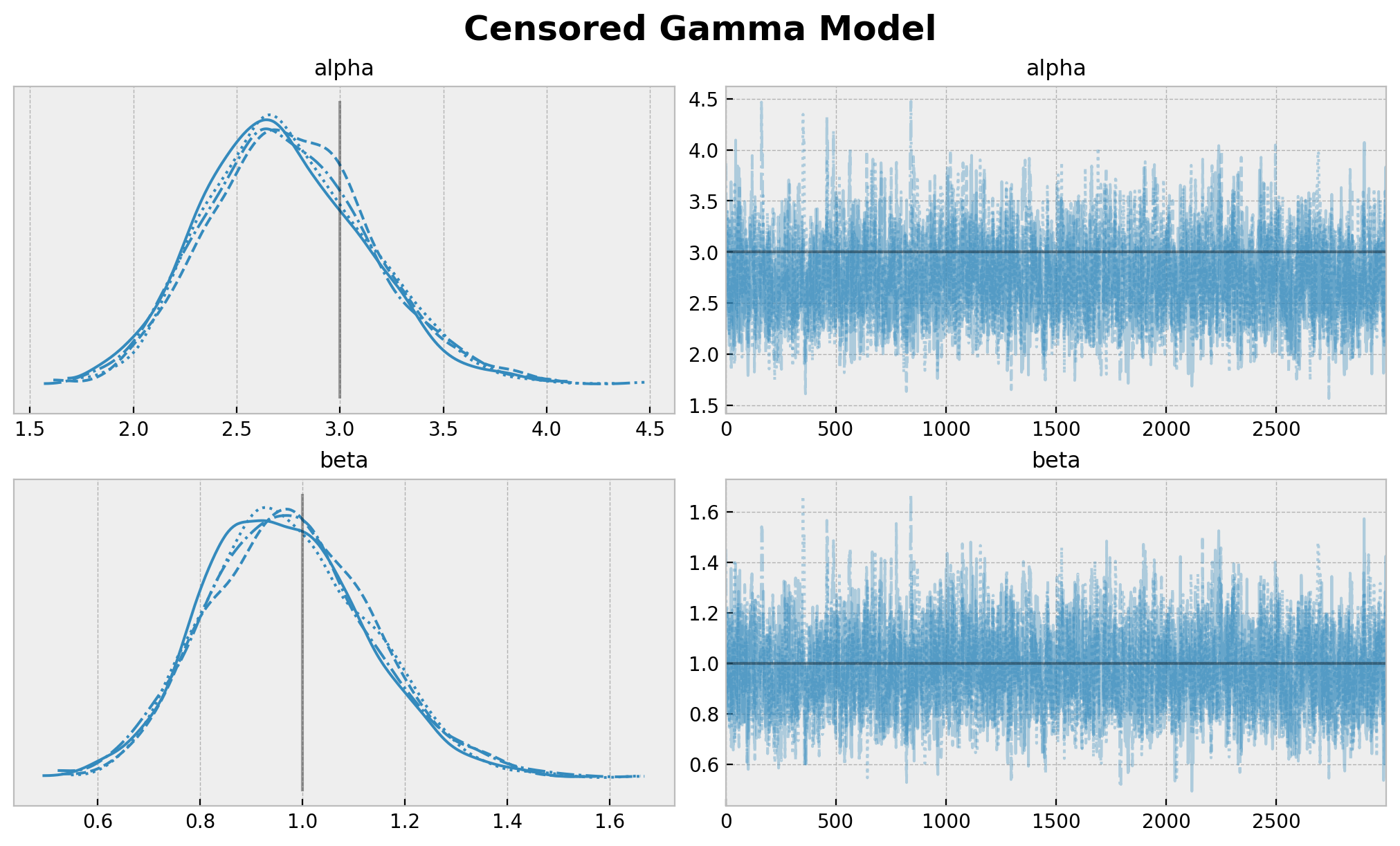
axes = az.plot_trace(
data=censored_gamma_idata,
compact=True,
lines=[
("alpha", {}, censored_gamma_data_params.alpha),
("beta", {}, censored_gamma_data_params.beta),
],
backend_kwargs={"figsize": (10, 6), "layout": "constrained"},
)
plt.gcf().suptitle("Censored Gamma Model", fontsize=18, fontweight="bold");
[13]:
axes = az.plot_posterior(
data=censored_gamma_idata,
ref_val=[censored_gamma_data_params.alpha, censored_gamma_data_params.beta],
round_to=3,
figsize=(12, 5),
)
plt.gcf().suptitle(
"Censored Gamma Model Parameters", fontsize=18, fontweight="bold", y=1.03
);
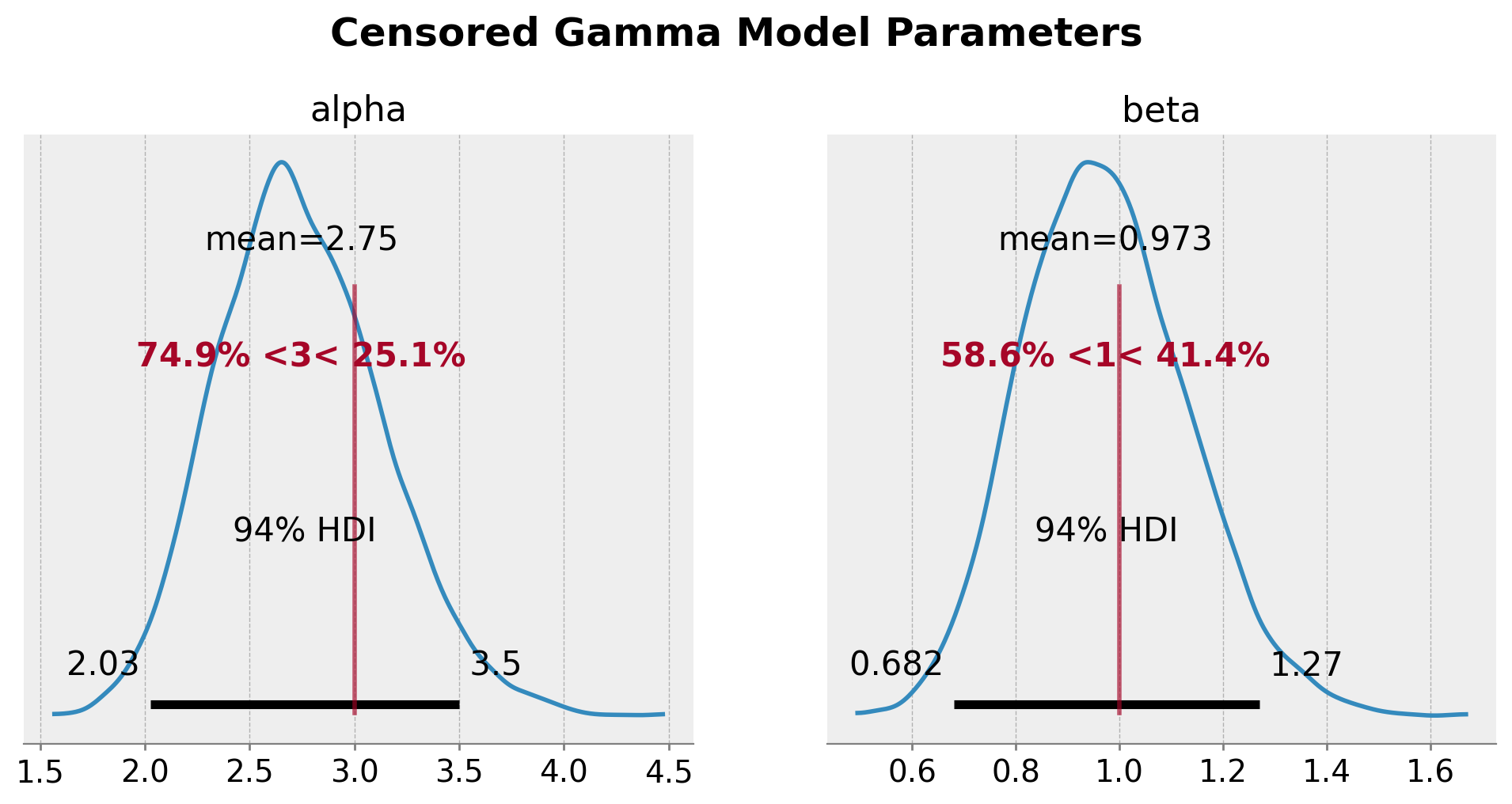
We clearly see that the true parameters are in correspond to the mean and mode of the posterior distribution. The censoring model is able to recover the true parameters.
As we did for the naive model, we visualize the inferred distribution and compare it with the true distribution from the data generating process.
[14]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_gamma_samples,
bins=20,
density=True,
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_gamma_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_gamma_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Gamma(
alpha=censored_gamma_data_params.alpha, beta=censored_gamma_data_params.beta
).plot_pdf(color="C0", ax=ax)
az.plot_kde(
censored_gamma_idata["posterior_predictive"]["obs"].to_numpy().flatten(),
plot_kwargs={"color": "C2", "label": "Posterior predictive"},
ax=ax,
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Censored Gamma Model (no clipping)", fontsize=16, fontweight="bold");
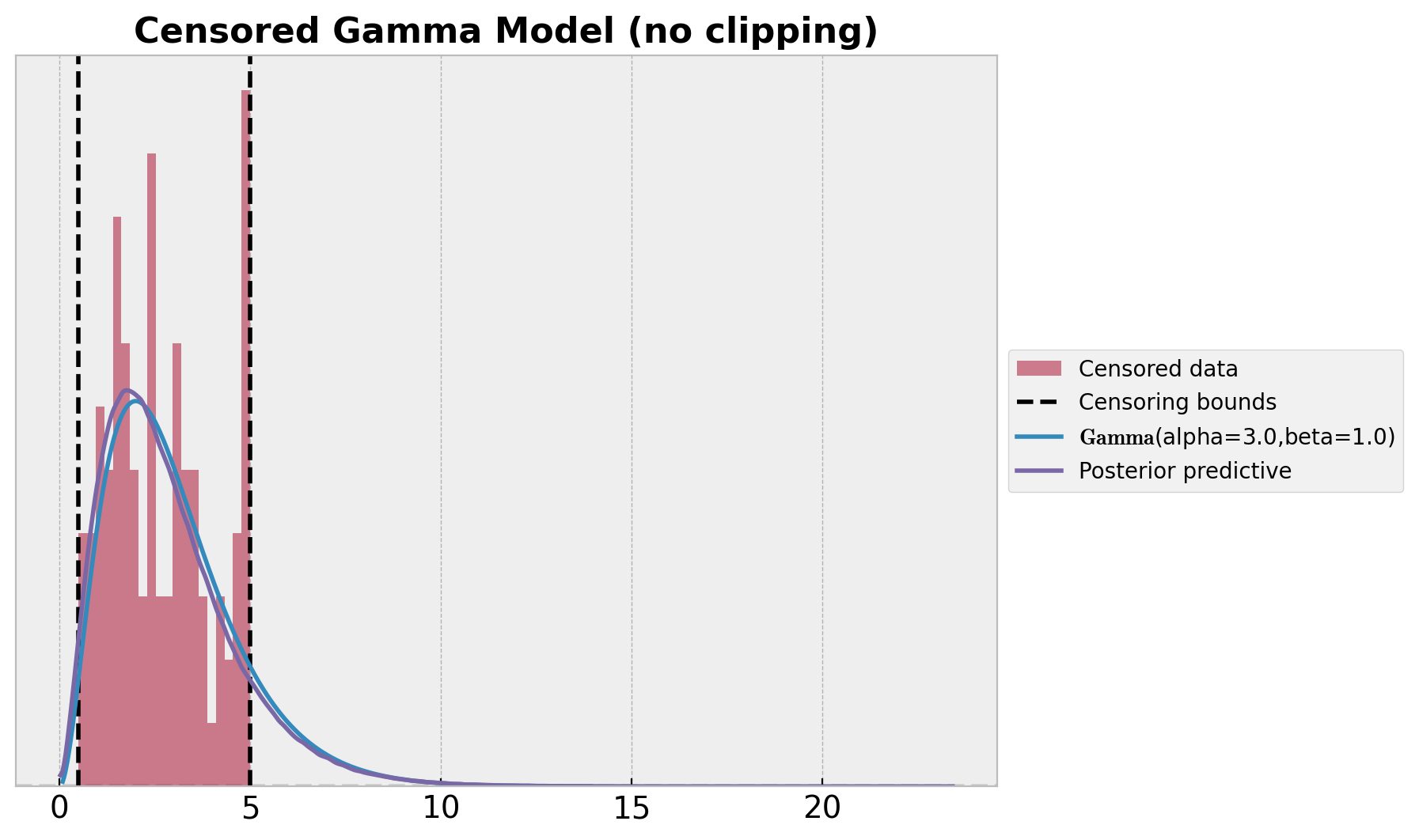
This looks much better than the naive model. However, there something wring as we are just sampling from the obs variable! We should not have posterior samples outside the censoring bounds. We can easily fix this by clipping the samples to the bounds.
[15]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_gamma_samples,
bins=20,
density=True,
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_gamma_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_gamma_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Gamma(
alpha=censored_gamma_data_params.alpha, beta=censored_gamma_data_params.beta
).plot_pdf(color="C0", ax=ax)
az.plot_kde(
censored_gamma_idata["posterior_predictive"]["obs"]
.clip(min=censored_gamma_data_params.lower, max=censored_gamma_data_params.upper)
.to_numpy()
.flatten(),
plot_kwargs={"color": "C2", "label": "Posterior predictive"},
ax=ax,
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Censored Gamma Model", fontsize=16, fontweight="bold");
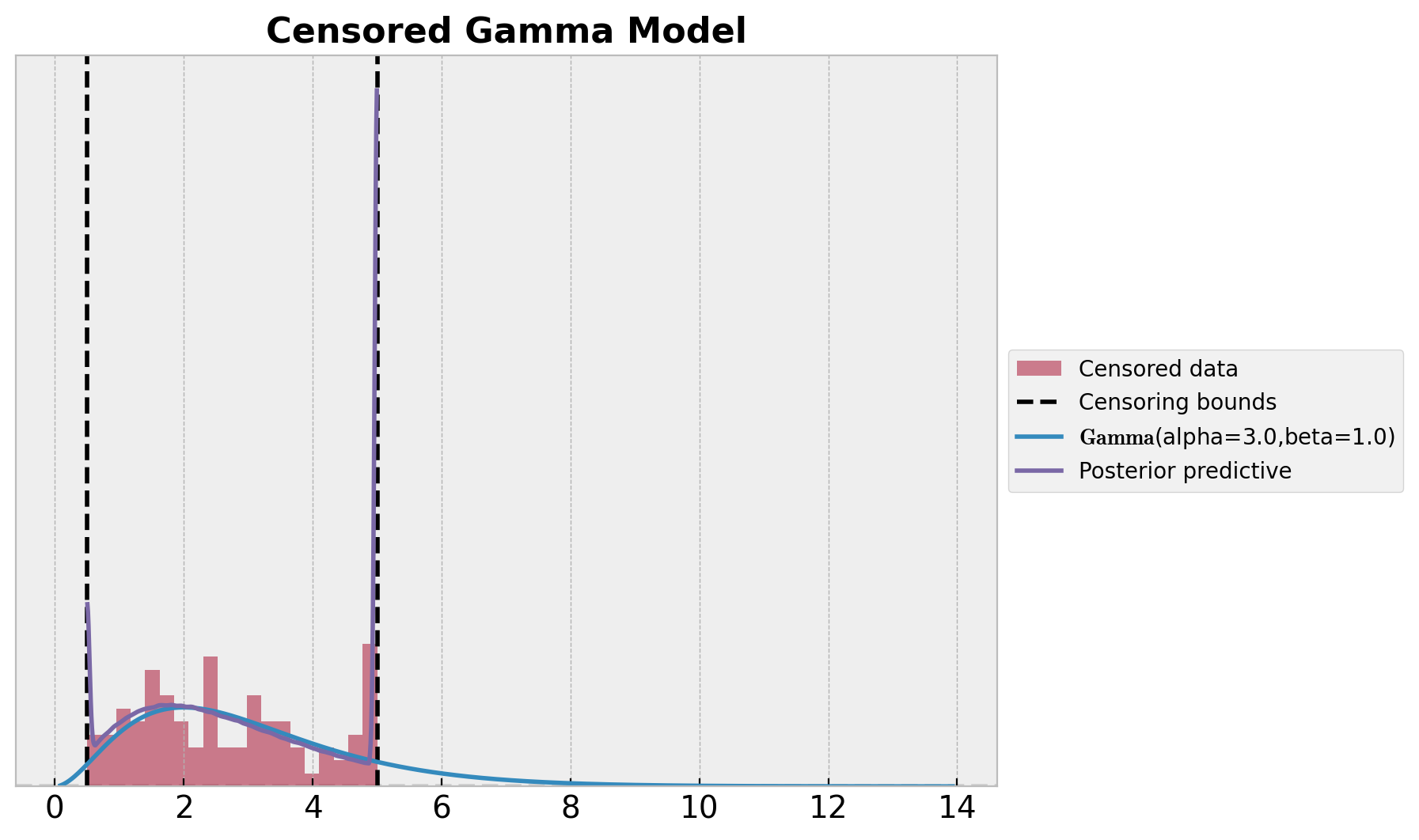
Part II: Discrete Distribution¶
In this second part we do the same as in the first part but for a discrete distribution. Again, we assume that we have a dataset of observations \(y\) that are censored from below and above at known thresholds. This time we assume the data follows a Poisson distribution (with parameter \(\lambda\)). We want to recover the true parameter \(\lambda\). The censoring model has the same structure as in the continuous case, but there is a small detail in the upper bound. We need to add term to to the truncation probability to account for the probability of the upper bound. Specifically we need to add the probability of the upper bound using the PDF.
Generate Censored Data¶
We generate data from a Poisson distribution and we clip the data to be between the thresholds lower and upper. We then plot the histogram of the data and the true Poisson distribution.
[16]:
class CensoredPoissonDataParams(BaseModel):
rate: float = Field(..., description="Rate parameter", gt=0)
lower: float = Field(..., description="Lower censoring bound", gt=0)
upper: float = Field(..., description="Upper censoring bound", gt=0)
n: int = Field(..., description="Number of samples", gt=0)
def generate_censored_poisson_samples(
rng_key: ArrayImpl, params: CensoredPoissonDataParams
) -> ArrayImpl:
raw_samples = dist.Poisson(rate=params.rate).sample(rng_key, (params.n,))
return jnp.clip(raw_samples, params.lower, params.upper)
censored_poisson_data_params = CensoredPoissonDataParams(
rate=1, lower=1, upper=4, n=100
)
rng_key, rng_subkey = random.split(rng_key)
censored_poisson_samples = generate_censored_poisson_samples(
rng_key=rng_subkey, params=censored_poisson_data_params
)
fig, ax = plt.subplots()
_ = ax.hist(
censored_poisson_samples,
bins=20,
density=True,
color="C1",
alpha=0.5,
label="Censored data",
align="left",
)
ax.axvline(censored_gamma_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_poisson_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Poisson(mu=censored_poisson_data_params.rate).plot_pdf(color="C0", ax=ax)
ax.set_title("Censored Poisson Sample Data", fontsize=16, fontweight="bold");
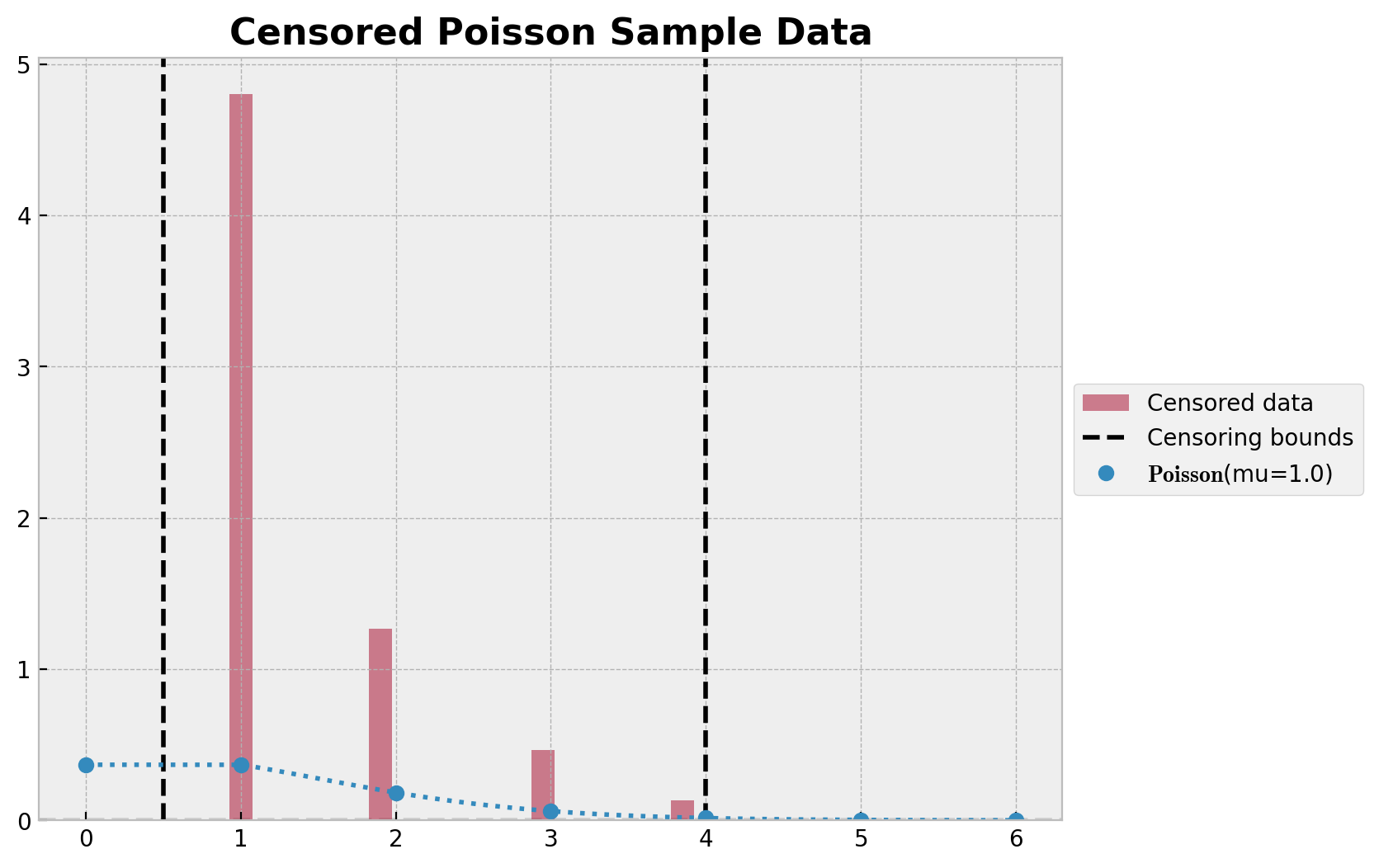
Naive Model¶
Just as in the continuous case, we start with a naive model that does not take into account the censoring component. We simply use a Poisson distribution with parameter \(\lambda\) to model the data.
[17]:
def poisson_model(y: ArrayImpl) -> None:
rate = numpyro.sample("rate", dist.Exponential(1.0))
numpyro.sample("obs", dist.Poisson(rate), obs=y)
poisson_kernel = NUTS(poisson_model)
poisson_mcmc = MCMC(
poisson_kernel,
num_warmup=inference_params.num_warmup,
num_samples=inference_params.num_samples,
num_chains=inference_params.num_chains,
)
rng_key, rng_subkey = random.split(rng_key)
poisson_mcmc.run(rng_key, y=censored_poisson_samples)
Compiling.. : 0%| | 0/5000 [00:00<?, ?it/s]
Running chain 0: 100%|██████████| 5000/5000 [00:02<00:00, 2123.00it/s]
Running chain 1: 100%|██████████| 5000/5000 [00:02<00:00, 2126.03it/s]
Running chain 2: 100%|██████████| 5000/5000 [00:02<00:00, 2129.97it/s]
Running chain 3: 100%|██████████| 5000/5000 [00:02<00:00, 2134.66it/s]
[18]:
poisson_predictive = Predictive(
model=poisson_model, posterior_samples=poisson_mcmc.get_samples()
)
rng_key, rng_subkey = random.split(rng_key)
poisson_posterior_predictive = poisson_predictive(rng_subkey, y=None)
poisson_idata = az.from_numpyro(posterior=poisson_mcmc)
poisson_idata.extend(az.from_numpyro(posterior_predictive=poisson_posterior_predictive))
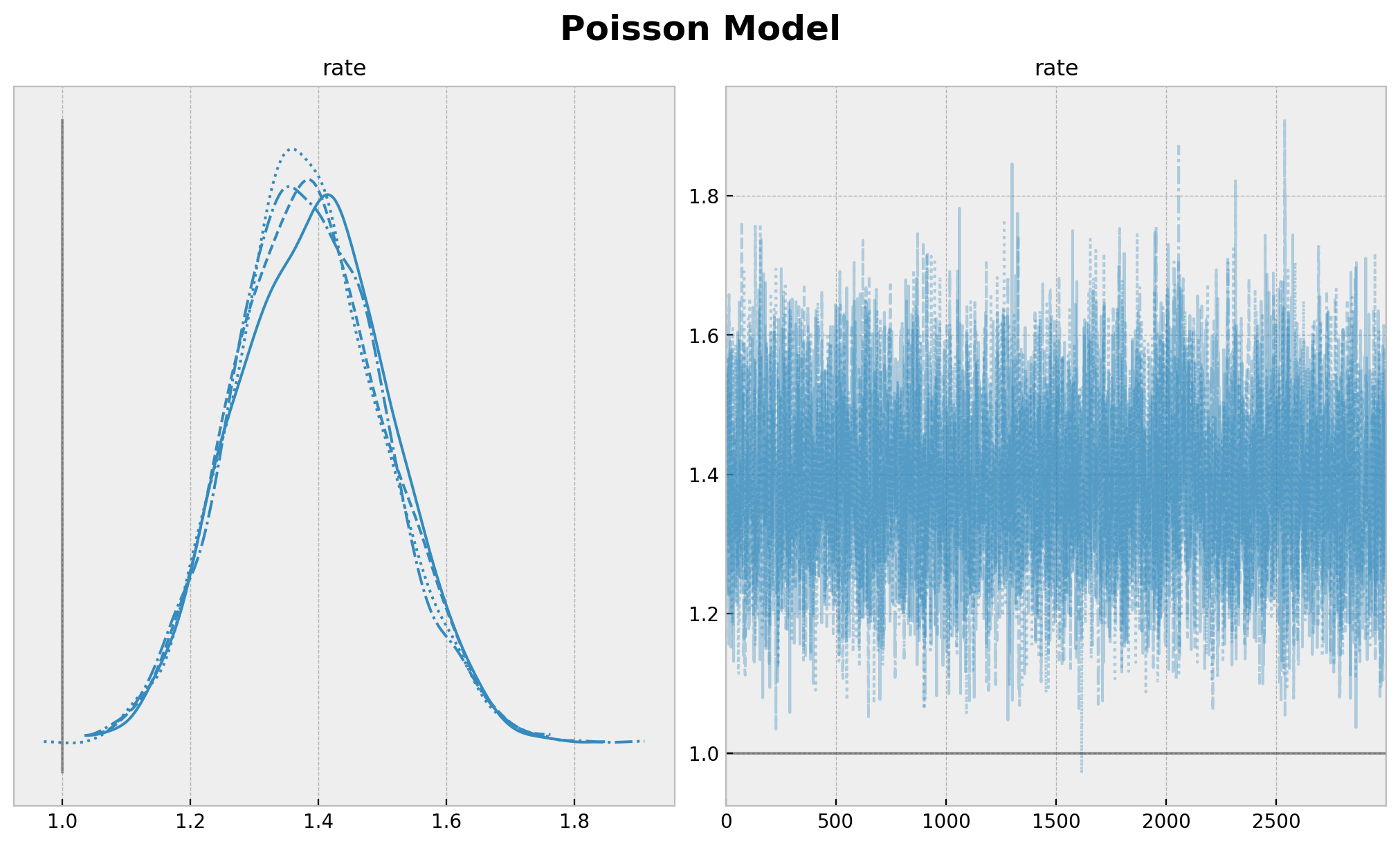
[19]:
axes = az.plot_trace(
data=poisson_idata,
compact=True,
lines=[("rate", {}, censored_poisson_data_params.rate)],
backend_kwargs={"figsize": (10, 6), "layout": "constrained"},
)
plt.gcf().suptitle("Poisson Model", fontsize=18, fontweight="bold");
[20]:
axes = az.plot_posterior(
data=poisson_idata,
ref_val=[censored_poisson_data_params.rate],
round_to=3,
figsize=(10, 6),
)
plt.gcf().suptitle("Poisson Model Parameter", fontsize=18, fontweight="bold");
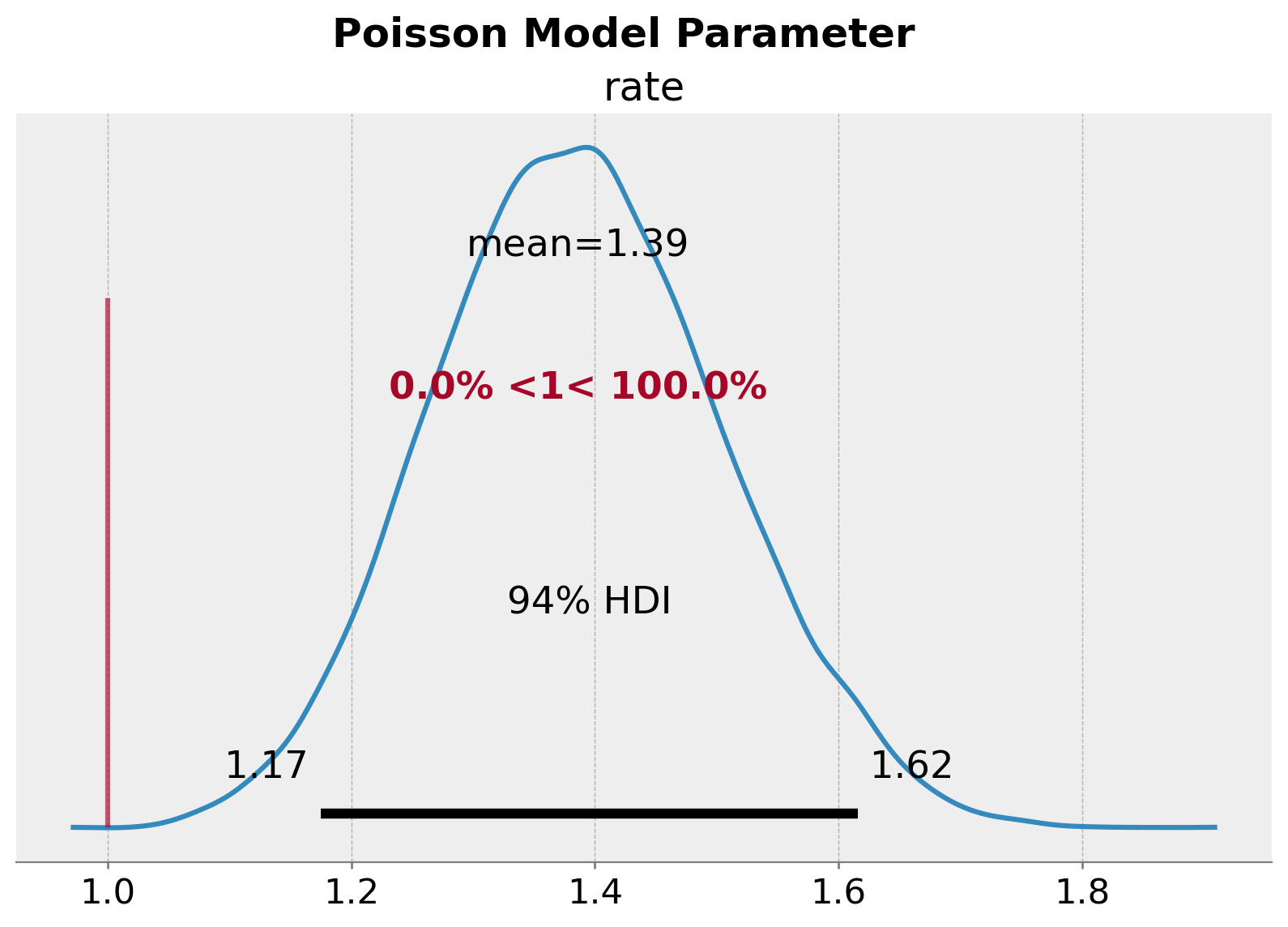
We clearly see a bias in the estimation of the parameter. The true value of the rate parameter \(\lambda\) is not even in the \(94\%\) HDI.
We can also take a look into the posterior predictive distribution.
[21]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_poisson_samples,
bins=20,
density=True,
align="left",
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_poisson_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_poisson_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Poisson(mu=censored_poisson_data_params.rate).plot_pdf(color="C0", ax=ax)
_ = ax.hist(
poisson_idata["posterior_predictive"]["obs"].to_numpy().flatten(),
bins=50,
density=True,
align="right",
color="C2",
alpha=0.5,
label="Censored data",
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Poisson Model", fontsize=16, fontweight="bold");
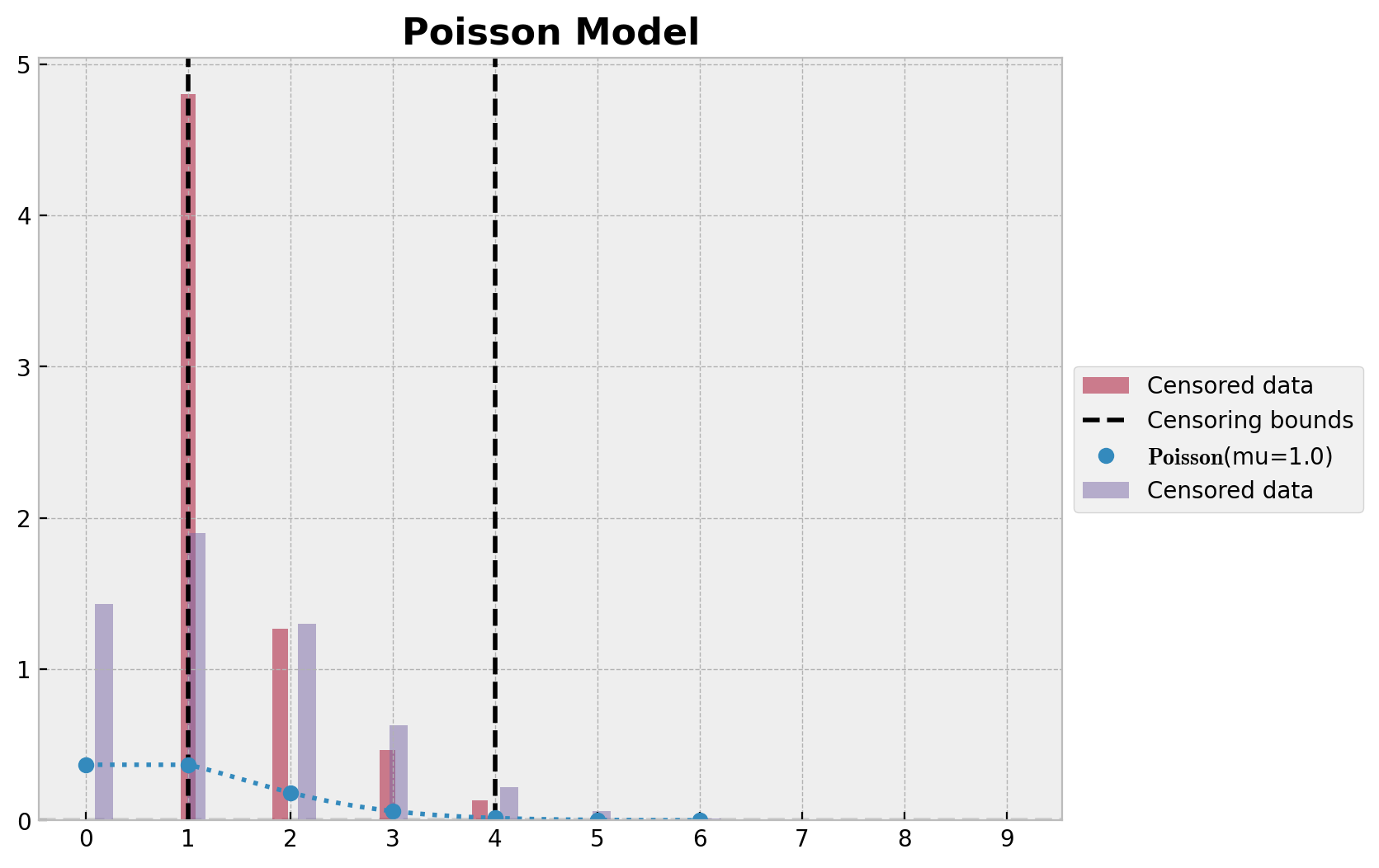
Censored Poisson Model¶
Now we work out the censored model. As before, we need to get the censoring labels to manage the likelihood components:
[22]:
truncation_label = get_truncation_label(
y=censored_poisson_samples,
lower=censored_poisson_data_params.lower,
upper=censored_poisson_data_params.upper,
)
Now, finally regarding the detail about the upper censoring component.
We want to consider the closed interval \(P(lower \leq y \leq upper)\).
For the upper interval we use \(1 - CDF(upper) = 1- P(y \leq upper) = P(y > upper)\), but we actually need \((P \geq upper)\).
Hence we need to add \(P(y= upper)\) in the upper truncation probability.
Observe that this discussion is irrelevant for the continuous case as the probability of a single point is zero so \(P(y > upper) = P(y \geq upper)\).
The implementation of the model should be clearer now.
[23]:
def censored_poisson_model(
y: ArrayImpl, lower: float, upper: float, truncation_label: ArrayImpl
) -> None:
rate = numpyro.sample("rate", dist.Exponential(1.0))
distribution = dist.Poisson(rate)
with mask(mask=truncation_label == -1):
truncation_prob_lower = distribution.cdf(lower)
numpyro.sample(
"truncated_label_lower", dist.Bernoulli(truncation_prob_lower), obs=1
)
with mask(mask=truncation_label == 0):
numpyro.sample("obs", distribution, obs=y)
with mask(mask=truncation_label == 1):
ccdf_upper = 1 - distribution.cdf(upper)
pmf_upper = jnp.exp(distribution.log_prob(upper))
truncation_prob_upper = ccdf_upper + pmf_upper
numpyro.sample(
"truncated_label_upper", dist.Bernoulli(truncation_prob_upper), obs=1
)
Remark: This was an important detail pointed out by Kyle Caron in his blog post “Modeling Anything With First Principles: Demand under extreme stockouts”.
We proceed to fit the model and compare the results with the true parameter.
[24]:
censored_poisson_kernel = NUTS(censored_poisson_model)
censored_poisson_mcmc = MCMC(
censored_poisson_kernel,
num_warmup=inference_params.num_warmup,
num_samples=inference_params.num_samples,
num_chains=inference_params.num_chains,
)
rng_key, rng_subkey = random.split(rng_key)
censored_poisson_mcmc.run(
rng_key,
y=censored_poisson_samples,
lower=censored_poisson_data_params.lower,
upper=censored_poisson_data_params.upper,
truncation_label=truncation_label,
)
Compiling.. : 0%| | 0/5000 [00:00<?, ?it/s]
Running chain 0: 100%|██████████| 5000/5000 [00:03<00:00, 1257.60it/s]
Running chain 1: 100%|██████████| 5000/5000 [00:03<00:00, 1259.63it/s]
Running chain 2: 100%|██████████| 5000/5000 [00:03<00:00, 1260.75it/s]
Running chain 3: 100%|██████████| 5000/5000 [00:03<00:00, 1261.95it/s]
[25]:
censores_poisson_predictive = Predictive(
model=censored_poisson_model,
posterior_samples=censored_poisson_mcmc.get_samples(),
return_sites=["obs"],
)
rng_key, rng_subkey = random.split(rng_key)
censored_poisson_posterior_predictive = censores_poisson_predictive(
rng_subkey,
y=None,
lower=censored_poisson_data_params.lower,
upper=censored_poisson_data_params.upper,
truncation_label=truncation_label,
)
censored_poisson_idata = az.from_numpyro(posterior=censored_poisson_mcmc)
censored_poisson_idata.extend(
az.from_numpyro(posterior_predictive=censored_poisson_posterior_predictive)
)
[26]:
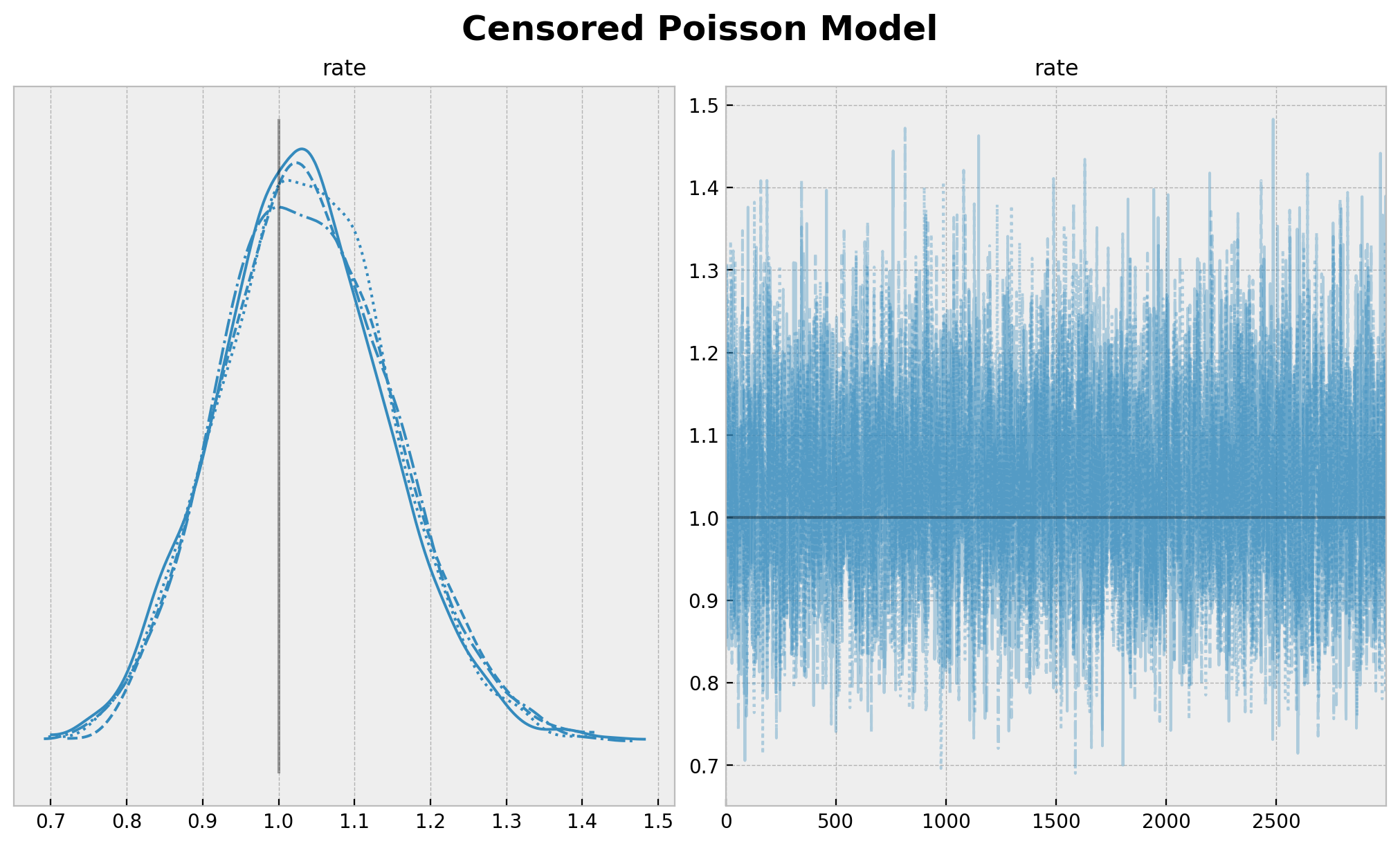
axes = az.plot_trace(
data=censored_poisson_idata,
compact=True,
lines=[("rate", {}, censored_poisson_data_params.rate)],
backend_kwargs={"figsize": (10, 6), "layout": "constrained"},
)
plt.gcf().suptitle("Censored Poisson Model", fontsize=18, fontweight="bold");
[27]:
axes = az.plot_posterior(
data=censored_poisson_idata,
ref_val=[censored_poisson_data_params.rate],
round_to=3,
figsize=(10, 6),
)
plt.gcf().suptitle("Censored Poisson Model Parameter", fontsize=18, fontweight="bold");
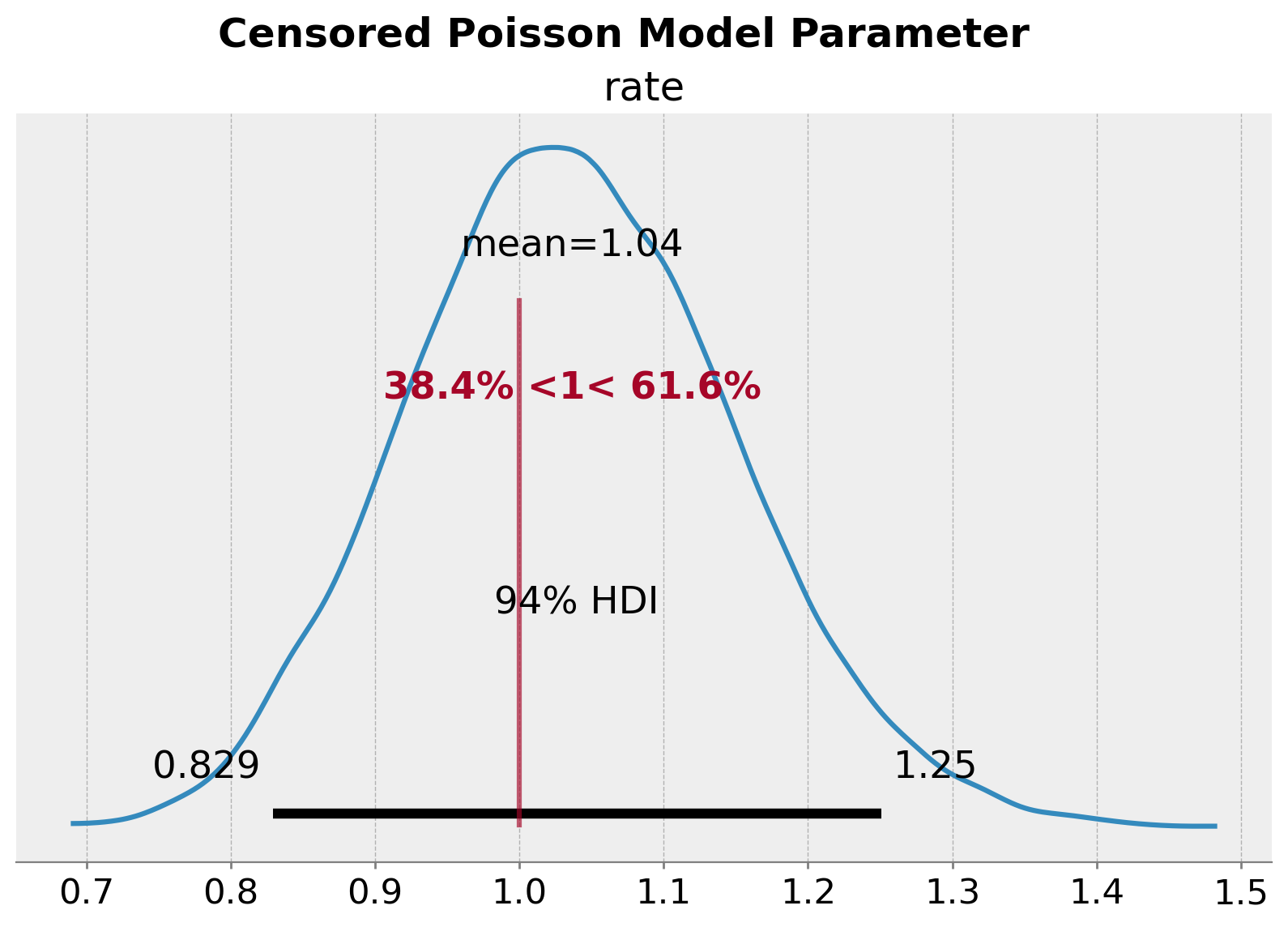
We see that we have recovered the true value of the rate parameter \(\lambda = 1\).
Here is the posterior predictive distribution:
[28]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_poisson_samples,
bins=20,
density=True,
align="left",
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_poisson_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_poisson_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Poisson(mu=censored_poisson_data_params.rate).plot_pdf(color="C0", ax=ax)
_ = ax.hist(
censored_poisson_idata["posterior_predictive"]["obs"].to_numpy().flatten(),
bins=50,
density=True,
align="right",
color="C2",
alpha=0.5,
label="Censored data",
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Censored Poisson Model (no clipping)", fontsize=16, fontweight="bold");
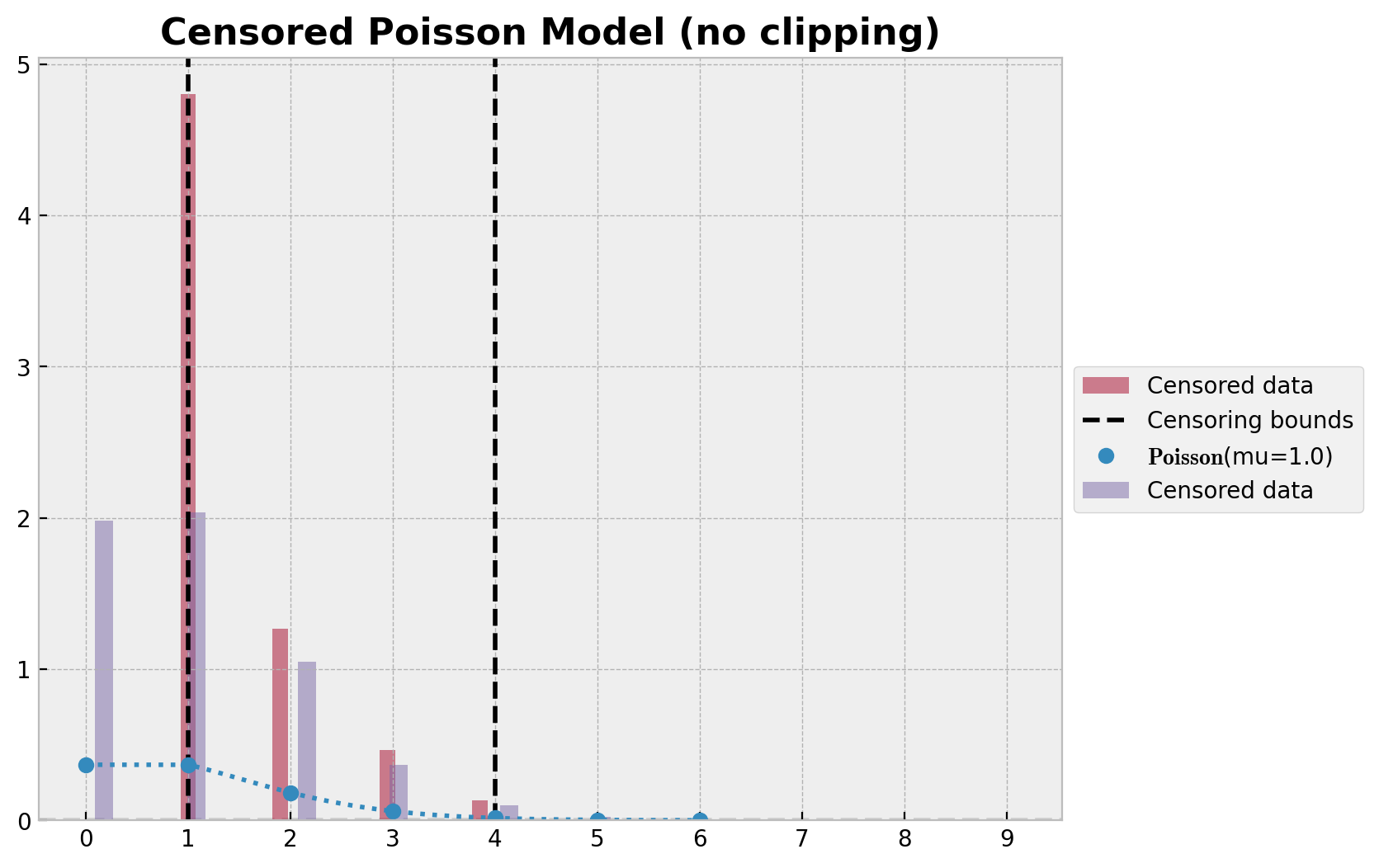
As before, to have a correct posterior predictive distribution we need to clip the samples to the bounds.
[29]:
fig, ax = plt.subplots()
_ = ax.hist(
censored_poisson_samples,
bins=20,
density=True,
align="left",
color="C1",
alpha=0.5,
label="Censored data",
)
ax.axvline(censored_poisson_data_params.lower, color="k", linestyle="--")
ax.axvline(
censored_poisson_data_params.upper,
color="k",
linestyle="--",
label="Censoring bounds",
)
pz.Poisson(mu=censored_poisson_data_params.rate).plot_pdf(color="C0", ax=ax)
_ = ax.hist(
censored_poisson_idata["posterior_predictive"]["obs"]
.clip(
min=censored_poisson_data_params.lower, max=censored_poisson_data_params.upper
)
.to_numpy()
.flatten(),
bins=20,
density=True,
align="right",
color="C2",
alpha=0.5,
label="Censored data",
)
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_title("Censored Poisson Model", fontsize=16, fontweight="bold");
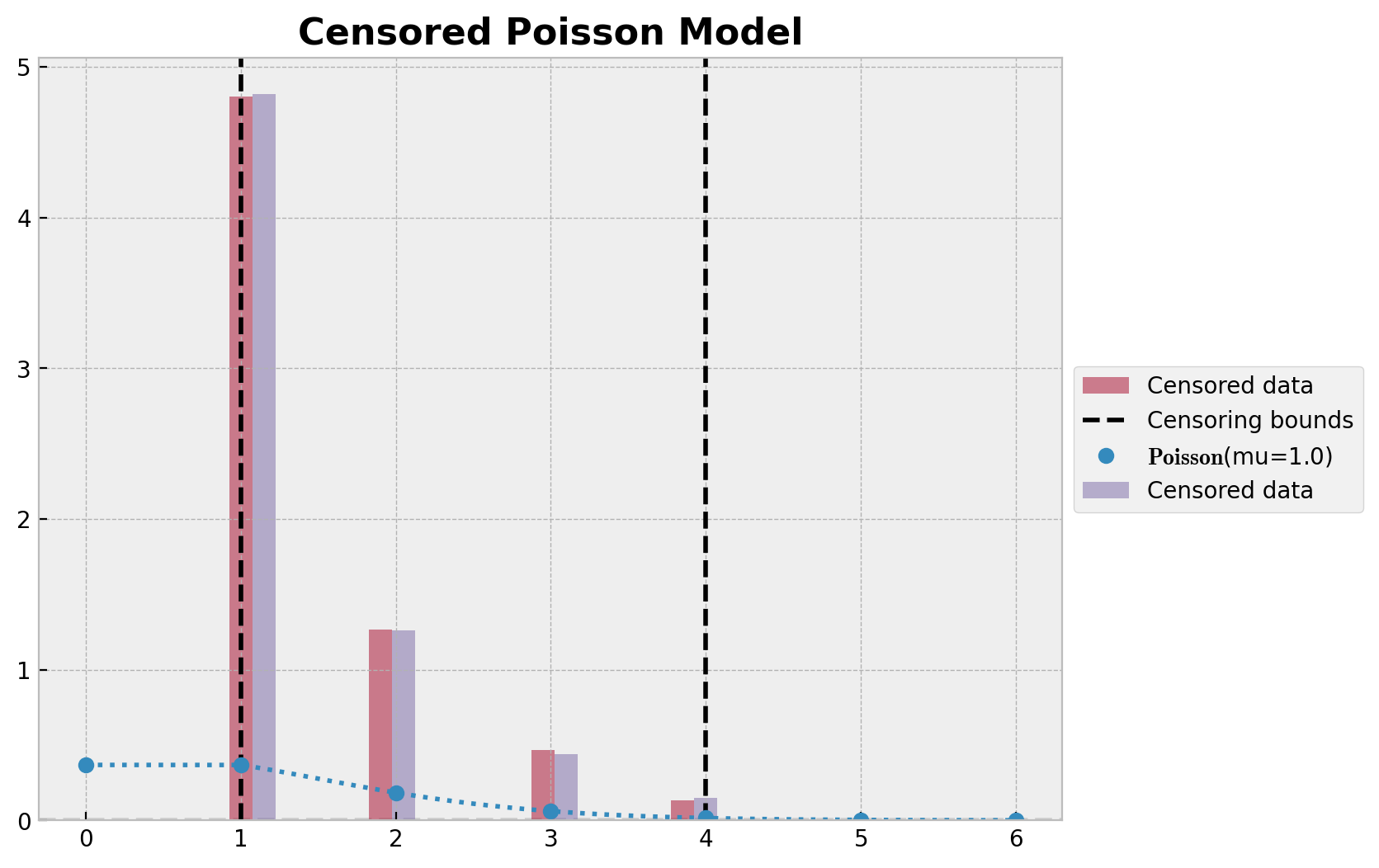
Here we see that the observed and predicted distributions match well.