Note
Click here to download the full example code
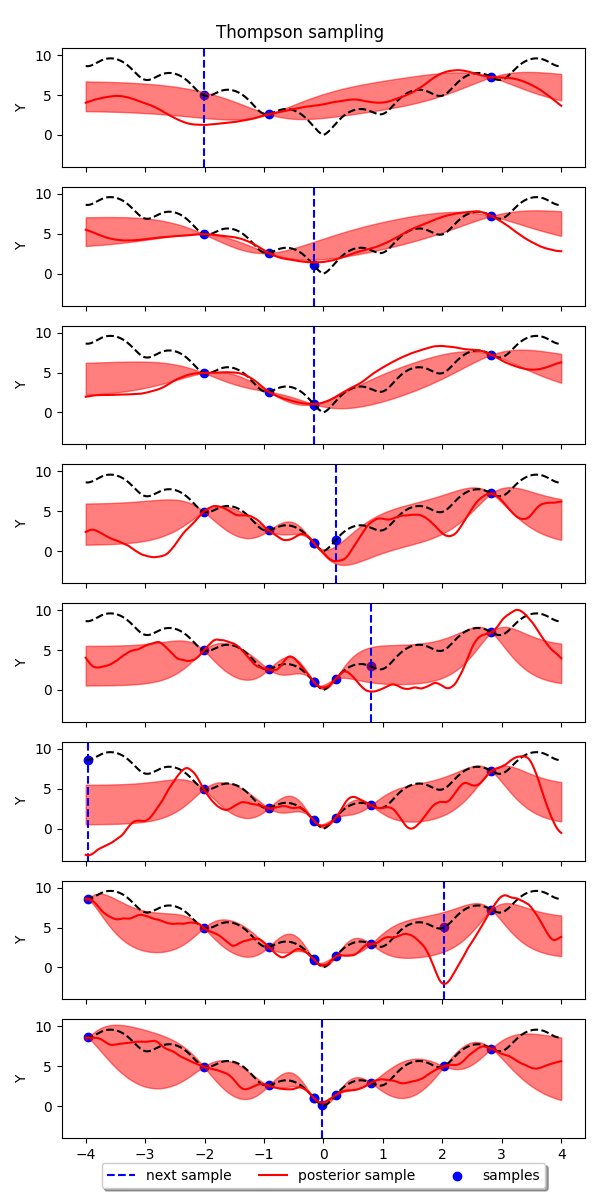
Example: Thompson sampling for Bayesian Optimization with GPs¶
In this example we show how to implement Thompson sampling for Bayesian optimization with Gaussian processes. The implementation is based on this tutorial: https://gdmarmerola.github.io/ts-for-bayesian-optim/
import argparse
import matplotlib.pyplot as plt
import numpy as np
import jax
import jax.numpy as jnp
import jax.random as random
from jax.scipy import linalg
import numpyro
import numpyro.distributions as dist
from numpyro.infer import SVI, Trace_ELBO
from numpyro.infer.autoguide import AutoDelta
numpyro.enable_x64()
# the function to be minimized. At y=0 to get a 1D cut at the origin
def ackley_1d(x, y=0):
out = (
-20 * jnp.exp(-0.2 * jnp.sqrt(0.5 * (x**2 + y**2)))
- jnp.exp(0.5 * (jnp.cos(2 * jnp.pi * x) + jnp.cos(2 * jnp.pi * y)))
+ jnp.e
+ 20
)
return out
# matern kernel with nu = 5/2
def matern52_kernel(X, Z, var=1.0, length=0.5, jitter=1.0e-6):
d = jnp.sqrt(0.5) * jnp.sqrt(jnp.power((X[:, None] - Z), 2.0)) / length
k = var * (1 + d + (d**2) / 3) * jnp.exp(-d)
if jitter:
# we are assuming a noise free process, but add a small jitter for numerical stability
k += jitter * jnp.eye(X.shape[0])
return k
def model(X, Y, kernel=matern52_kernel):
# set uninformative log-normal priors on our kernel hyperparameters
var = numpyro.sample("var", dist.LogNormal(0.0, 1.0))
length = numpyro.sample("length", dist.LogNormal(0.0, 1.0))
# compute kernel
k = kernel(X, X, var, length)
# sample Y according to the standard gaussian process formula
numpyro.sample(
"Y",
dist.MultivariateNormal(loc=jnp.zeros(X.shape[0]), covariance_matrix=k),
obs=Y,
)
class GP:
def __init__(self, kernel=matern52_kernel):
self.kernel = kernel
self.kernel_params = None
def fit(self, X, Y, rng_key, n_step):
self.X_train = X
# store moments of training y (to normalize)
self.y_mean = jnp.mean(Y)
self.y_std = jnp.std(Y)
# normalize y
Y = (Y - self.y_mean) / self.y_std
# setup optimizer and SVI
optim = numpyro.optim.Adam(step_size=0.005, b1=0.5)
svi = SVI(
model,
guide=AutoDelta(model),
optim=optim,
loss=Trace_ELBO(),
X=X,
Y=Y,
)
params, _ = svi.run(rng_key, n_step)
# get kernel parameters from guide with proper names
self.kernel_params = svi.guide.median(params)
# store cholesky factor of prior covariance
self.L = linalg.cho_factor(self.kernel(X, X, **self.kernel_params))
# store inverted prior covariance multiplied by y
self.alpha = linalg.cho_solve(self.L, Y)
return self.kernel_params
# do GP prediction for a given set of hyperparameters. this makes use of the well-known
# formula for gaussian process predictions
def predict(self, X, return_std=False):
# compute kernels between train and test data, etc.
k_pp = self.kernel(X, X, **self.kernel_params)
k_pX = self.kernel(X, self.X_train, **self.kernel_params, jitter=0.0)
# compute posterior covariance
K = k_pp - k_pX @ linalg.cho_solve(self.L, k_pX.T)
# compute posterior mean
mean = k_pX @ self.alpha
# we return both the mean function and the standard deviation
if return_std:
return (
(mean * self.y_std) + self.y_mean,
jnp.sqrt(jnp.diag(K * self.y_std**2)),
)
else:
return (mean * self.y_std) + self.y_mean, K * self.y_std**2
def sample_y(self, rng_key, X):
# get posterior mean and covariance
y_mean, y_cov = self.predict(X)
# draw one sample
return jax.random.multivariate_normal(rng_key, mean=y_mean, cov=y_cov)
# our TS-GP optimizer
class ThompsonSamplingGP:
"""Adapted to numpyro from https://gdmarmerola.github.io/ts-for-bayesian-optim/"""
# initialization
def __init__(
self, gp, n_random_draws, objective, x_bounds, grid_resolution=1000, seed=123
):
# Gaussian Process
self.gp = gp
# number of random samples before starting the optimization
self.n_random_draws = n_random_draws
# the objective is the function we're trying to optimize
self.objective = objective
# the bounds tell us the interval of x we can work
self.bounds = x_bounds
# interval resolution is defined as how many points we will use to
# represent the posterior sample
# we also define the x grid
self.grid_resolution = grid_resolution
self.X_grid = np.linspace(self.bounds[0], self.bounds[1], self.grid_resolution)
# also initializing our design matrix and target variable
self.X = np.array([])
self.y = np.array([])
self.rng_key = random.PRNGKey(seed)
# fitting process
def fit(self, X, y, n_step):
self.rng_key, subkey = random.split(self.rng_key)
# fitting the GP
self.gp.fit(X, y, rng_key=subkey, n_step=n_step)
# return the fitted model
return self.gp
# choose the next Thompson sample
def choose_next_sample(self, n_step=2_000):
# if we do not have enough samples, sample randomly from bounds
if self.X.shape[0] < self.n_random_draws:
self.rng_key, subkey = random.split(self.rng_key)
next_sample = random.uniform(
subkey, minval=self.bounds[0], maxval=self.bounds[1], shape=(1,)
)
# define dummy values for sample, mean and std to avoid errors when returning them
posterior_sample = np.array([np.mean(self.y)] * self.grid_resolution)
posterior_mean = np.array([np.mean(self.y)] * self.grid_resolution)
posterior_std = np.array([0] * self.grid_resolution)
# if we do, we fit the GP and choose the next point based on the posterior draw minimum
else:
# 1. Fit the GP to the observations we have
self.gp = self.fit(self.X, self.y, n_step=n_step)
# 2. Draw one sample (a function) from the posterior
self.rng_key, subkey = random.split(self.rng_key)
posterior_sample = self.gp.sample_y(subkey, self.X_grid)
# 3. Choose next point as the optimum of the sample
which_min = np.argmin(posterior_sample)
next_sample = self.X_grid[which_min]
# let us also get the std from the posterior, for visualization purposes
posterior_mean, posterior_std = self.gp.predict(
self.X_grid, return_std=True
)
# let us observe the objective and append this new data to our X and y
next_observation = self.objective(next_sample)
self.X = np.append(self.X, next_sample)
self.y = np.append(self.y, next_observation)
# returning values of interest
return (
self.X,
self.y,
self.X_grid,
posterior_sample,
posterior_mean,
posterior_std,
)
def main(args):
gp = GP(kernel=matern52_kernel)
# do inference
thompson = ThompsonSamplingGP(
gp, n_random_draws=args.num_random, objective=ackley_1d, x_bounds=(-4, 4)
)
fig, axes = plt.subplots(
args.num_samples - args.num_random, 1, figsize=(6, 12), sharex=True, sharey=True
)
for i in range(args.num_samples):
(
X,
y,
X_grid,
posterior_sample,
posterior_mean,
posterior_std,
) = thompson.choose_next_sample(
n_step=args.num_step,
)
if i >= args.num_random:
ax = axes[i - args.num_random]
# plot training data
ax.scatter(X, y, color="blue", marker="o", label="samples")
ax.axvline(
X_grid[posterior_sample.argmin()],
color="blue",
linestyle="--",
label="next sample",
)
ax.plot(X_grid, ackley_1d(X_grid), color="black", linestyle="--")
ax.plot(
X_grid,
posterior_sample,
color="red",
linestyle="-",
label="posterior sample",
)
# plot 90% confidence level of predictions
ax.fill_between(
X_grid,
posterior_mean - posterior_std,
posterior_mean + posterior_std,
color="red",
alpha=0.5,
)
ax.set_ylabel("Y")
if i == args.num_samples - 1:
ax.set_xlabel("X")
plt.legend(
loc="upper center",
bbox_to_anchor=(0.5, -0.15),
fancybox=True,
shadow=True,
ncol=3,
)
fig.suptitle("Thompson sampling")
fig.tight_layout()
plt.show()
if __name__ == "__main__":
assert numpyro.__version__.startswith("0.12.1")
parser = argparse.ArgumentParser(description="Thompson sampling example")
parser.add_argument(
"--num-random", nargs="?", default=2, type=int, help="number of random draws"
)
parser.add_argument(
"--num-samples",
nargs="?",
default=10,
type=int,
help="number of Thompson samples",
)
parser.add_argument(
"--num-step",
nargs="?",
default=2_000,
type=int,
help="number of steps for optimization",
)
parser.add_argument("--device", default="cpu", type=str, help='use "cpu" or "gpu".')
args = parser.parse_args()
numpyro.set_platform(args.device)
main(args)